Em Geologia do Petróleo, Permeabilidade Relativa é uma expressão sem dimensão criada para adaptar a Equação de Darcy às condições de fluxo multifásico na indústria do petróleo.

 

A permeabilidade relativa é a razão da permeabilidade efetiva de um fluido específico em uma saturação específica para a permeabilidade absoluta desse fluido na saturação total.

 

Exemplo, se um único fluido está presente em uma rocha, sua permeabilidade relativa é 1,0.

 

O cálculo da permeabilidade relativa permite a comparação das diferentes habilidades dos fluidos em fluir na presença um do outro, uma vez que a presença de mais de um fluido geralmente inibe o fluxo.

 

Em Inteligência Artificial (IA, na sigla em Inglês) e Aprendizado da Máquina, programas de computador e instrumentos de automação poderiam replicar tarefas humanas com mais velocidade, menor índice de erro e menor custo final, claro.

 

Vamos ao Estudo de Caso.

 

 

Resumo

 

O presente trabalho trata-se de um relatório para o case de sucesso na aplicação de algoritmos de Inteligência Artificial para predizer propriedades petrofísicas de poços de petróleo, mais precisamente obter a curva de permeabilidade relativa, a partir de dados de perfis geofísicos.

 

Utilizando técnicas de Machine Learning embarcadas em um Software Web na modalidade de Software as a Service (SaaS), essa proposta consiste em uma solução customizada para o cliente, capaz de estimar com confiança as curvas de interesse, diminuindo os riscos de exploração, minimizando os custos e auxiliando na tomada de decisão, além de possuir a possibilidade de atualização contínua dos modelos preditivos.

 

Com esta tecnologia, a QuantaGeo fornece um sistema que não só aprende padrões com dados, como permite um ajuste fino dos modelos à medida que novas bases de dados sejam utilizadas para treinamento do algoritmo e mantendo sempre o máximo padrão de segurança de dados.

 

O sistema permite também, caso desejável, que os modelos treinados sejam exportados para que possam ser utilizados em softwares proprietários e em outras aplicações de interesse do cliente, através de técnicas de transfer learning e online learning, aumentando ainda mais sua aplicabilidade no ramo da indústria do petróleo.

 

 

1- Introdução

 

Em vias tradicionais, ensaios complexos de escoamento em meio poroso para medir permeabilidade relativa demandam meses e exigem amostras de rocha e fluido representativos.

 

Tal procedimento, no entanto, é até então imprescindível, diante do impacto que estas informações contribuem para a análise e previsão do comportamento do escoamento de fluidos no reservatório.

 

Com um reservatório avaliado corretamente através de tais propriedades, pode-se definir com maior segurança o potencial de produção, maximizar a produção de hidrocarbonetos, minimizar os riscos, além de outros fatores.

 

Na revolução dos dados, também conhecida como a Indústria 4.0, a modernização, otimização de processos e extração de valor nos dados é não só desejável, mas sim um pilar para o desenvolvimento.

 

Com esse enfoque, a QuantaGeo tomou como desafio utilizar a extensa base de dados existente de perfis geofísicos de poços de petróleo e, aplicando algoritmos de Machine Learning, técnicas de análise de dados e tecnologias de desenvolvimento de Software as a Service (SaaS), desenvolveu soluções altamente robustas e escaláveis para reduzir custos e otimizar o processo de tomada de decisão na perfuração de poços de petróleo.

 

Dentre as tecnologias utilizadas na evolução do produto inovador aqui relatado, foi utilizada a linguagem de programação Python bem como suas principais bibliotecas open source para ciência de dados e aprendizagem de máquina.

 

Nas seções a seguir são explorados, além de um breve referencial teórico, a qualidade técnica e os resultados obtidos pelos diferentes algoritmos de Machine Learning aplicados, que resultam no desenvolvimento de um produto de software com objetivo de reduzir o tempo de estimativa de curvas de permeabilidade relativa.

 

 

2- Referencial Teórico

 

Do ponto de vista técnico, existem três tipos de permeabilidade, sendo importante fazer distinção entre as mesmas, uma vez que estas fornecem informações diferentes acerca do modo como os fluidos escoam no reservatório.

 

A permeabilidade absoluta se refere à capacidade de transmissão de um fluido quando a rocha é saturada apenas com um fluido. Por sua vez, a permeabilidade efetiva diz respeito à capacidade de escoamento de um fluido na presença de outro, podendo se referir às fases óleo (k-o), gás (k-g) ou água (k-w).

 

Por fim, a permeabilidade relativa pode ser expressa como um número entre 0 e 1.0 que consiste na relação entre a permeabilidade efetiva de uma rocha, parcialmente saturada por um fluido, e uma permeabilidade de referência, geralmente a absoluta.

 

A permeabilidade relativa pode ser referir também à àgua (kr-w), ao óleo (kr-o) ou ao gás (kr-g).

 

As curvas de permeabilidade relativa são valores importantes nas simulações numéricas de reservatórios, pois auxiliam na descrição da interação entre fluidos em um meio poroso no contexto de um sistema multifásico.

 

Usualmente, para obtenção dessas curvas são realizados ensaios laboratoriais em amostras de rochas reservatório que buscam reproduzir os fenômenos de deslocamentos de fluidos que ocorrem nas rochas.

 

Essas curvas, porém, levam um tempo demasiado longo para serem obtidas em laboratório, impedindo que as mesmas possam prover as informações necessárias para entendimento do escoamento de fluidos no reservatório em um curto prazo.

 

 

3- Inteligência de Dados: Algoritimos de Machine Lerarning Aplicados

 

Duas aplicações foram desenvolvidas buscando realizar a predição de permeabilidade absoluta (K em mD).

 

Cada uma delas possui foco em um conjunto específico de rochas e um contexto de bacia sedimentar distinto.

 

Além de dados de profundidade e litologia interpretada, as bases de dados destes poços eram compostas por caliper, bit size, raios gama, resistividade (RT10, RT20, RT30, RT60 e RT90), neutrão, densidade e sônico, e somente para o segundo caso haviam dados de ressonância magnética nuclear (RMN).

 

Em ambos os casos, os valores de K foram estimados inicialmente através de estimativas a partir da porosidade, e, quando presente o perfil de RMN, a partir do método SDR.

 

Tal conjunto de dados foi passado para os algoritmos descritos adiante, buscando demonstrar sua capacidade de modelar os valores de K a partir de dados perfis.

 

3.1 Previsão de Permeabilidade em Arenitos

 

Para a primeira aplicação foram utilizadas bases de dados de poços perfurados em uma mesma bacia on-shore, dos quais foram filtrados apenas os dados mensurados na profundidade na qual a litologia interpretada se referia a arenitos (ARN).

 

Aleatoriamente, foram sorteados 66,67% dos poços para utilizar como treinamento dos modelos de Machine Learning, separando os 33,33% restante dos poços para utilizar como teste.

 

O histograma que mostra a distribuição de frequências dos valores de K existentes na base de dados de treino pode ser visualizado a seguir, na Figura 1:

 

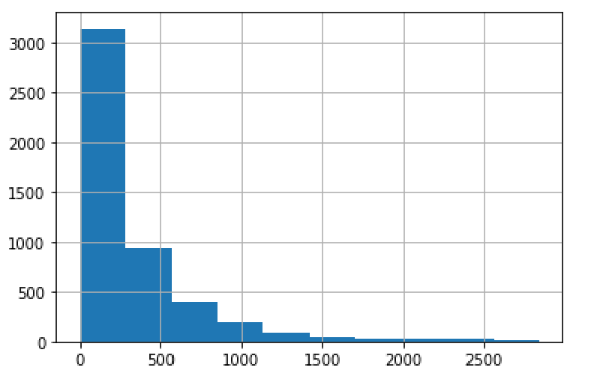
Figura 1 – Historograma para K na base de dados treino

 

Nota-se pelo histograma que há uma assimetria perceptível nos dados, que estão concentrados sobretudo na região de menor magnitude da permeabilidade.

 

Para evitar possíveis problemas de desbalanceamento nos dados e poder gerar uma maior variedade de modelos, foi gerada uma curva auxiliar, aplicando uma transformação logarítmica nos dados de permeabilidade.

 

Nomearemos esta curva por log(K).

 

A descrição matemática para a geração desta curva pode ser entendida no procedimento da Equação I:

 

log(K)i = log10(Ki + 1)                                                     (I)

 

Para cada “i” no domínio da curva de K

 

Aplicada esta transformação, o histograma para os dados da curva de log(K) pode ser visualizado como ilustra a Figura 2:

 

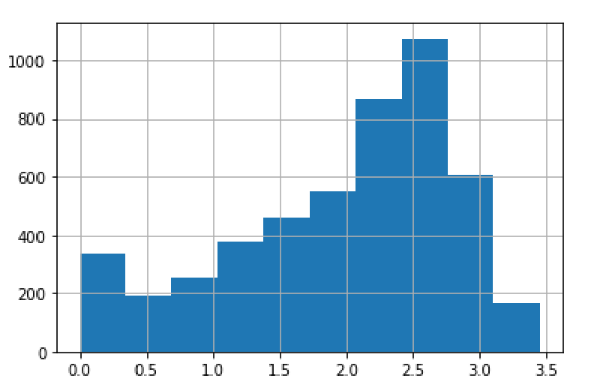
Figura 2 – Histograma para log(K)

 

Com essa distribuição, após análise técnica de variados modelos, a equipe conseguiu melhorar as aplicações em diferentes cenários, dependendo do algoritmo de Machine Learning utilizado.

 

Dentre estes algoritmos, relata-se aqui alguns que foram criteriosamente selecionados, visando o desenvolvimento de soluções teoricamente coerentes, escaláveis e eficientes, sendo eles: 

 

1 – Support Vector Regression (SVR);

2 – Decision Tree Regressor;

3 – Random Forest Regressor; e

4 – Multi-layer Perceptron (MLP).

 

A seguir, são definidos e explorados os resultados para cada uma destas aplicações.

 

Ao fim de cada seção, são apresentados de maneira gráfica os resultados obtidos e, logo em seguida, as métricas de erro utilizadas para avaliar o desempenho dos modelos, sendo elas o Coeficiente de Correlação (R), Erro Médio Absoluto e Erro Médio Quadrático.

 

3.1.1 Support Vector Regression (SVR)

 

SVR, algoritmo baseado no modelo clássico de Support Vector Machine (SVM), é um modelo de Machine Learning com elevado histórico de aplicação na própria indústria do petróleo, englobando estudos complexos com aplicação em predição de propriedades do óleo (EL-SEBAKHY et al., 2007) e até para predizer a própria porosidade e permeabilidade da rocha através de perfis geofísicos (AL-ANAZI e GATES, 2012). 

 

Em uma primeira aplicação, utilizando o algoritmo SVR, o problema é modelado relacionando a permeabilidade, obtida através de análise petrofísica, com os valores das curvas de perfilagem obtidos para cada profundidade na base de dados.

 

Deste modo, modelou-se o problema predizendo o logaritmo da curva de permeabilidade, nomeada acima como curva log(K).

 

Com esta aplicação, após modelar o problema para predizer o log(K) e realizar a transformação inversa para identificar o valor efetivo da permeabilidade, obtém-se, para o mesmo poço teste, os resultados ilustrados a seguir:

 

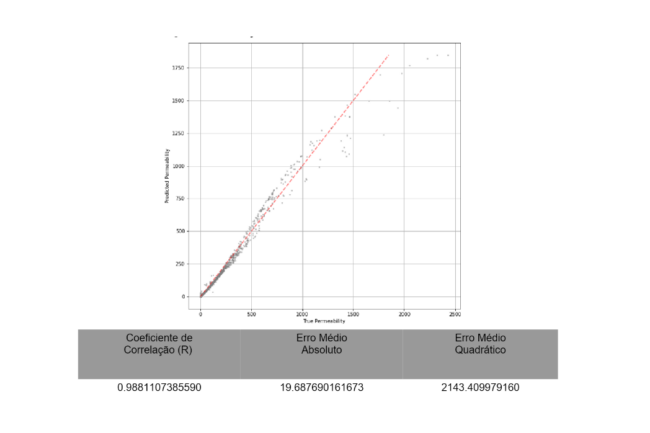
Figura 3 – Predição de Permeabilidade Utilizando SVR

 

3.1.2 Decision Tree Regressor

 

Este algoritmo clássico e com relativamente baixíssimo custo computacional quando comparado a algoritmos mais avançados, baseia-se na observação dos dados e no aprendizado estatístico e automático para criar uma estrutura de dados altamente escalável capaz de resolver problemas difíceis de serem modelados algebricamente.

 

Também com vasta aplicação científica na área de petróleo, ele é capaz de resolver de maneira eficiente problemas complexos, tais como classificação de dados sísmicos (WENRUI et al., 2018) e auxiliar na interpretação de modelos geológicos aplicáveis para exploração de petróleo e gás (ROUBICKOVA; BROWN; e BROWN, 2019).

Com este algoritmo, os dados foram modelados de maneira similar à primeira aplicação descrita utilizando o algoritmo SVR no tópico anterior, colocando a curva de permeabilidade em função das curvas de logs de Petrofísica analisadas, obtendo os seguintes resultados:

 

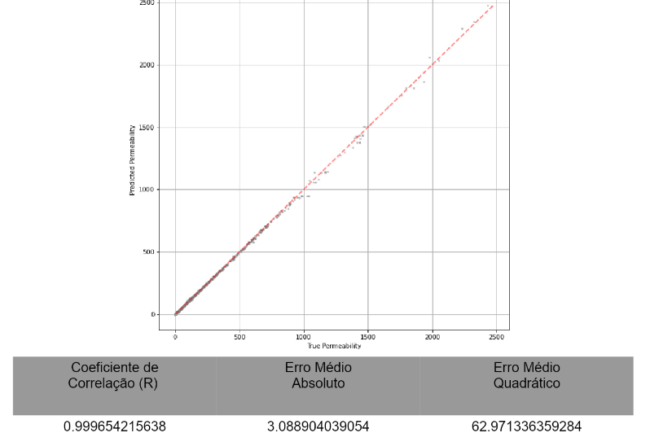
Figura 4 – Predição de Permeabilidade Utilizando Decision Tree

 

Para este ajuste, a qualidade dos resultados obtidos foi extremamente vantajosa, obtendo coeficiente de correlação superior à 99,96% e erro médio absoluto de aproximadamente 3,09, com nenhum dado ficando distante da curva destacada em vermelho, que representa o resultado pefeito para o modelo.

 

Resultados similares mas levemente inferiores também foram obtidos ao utilizar a predição do log(K), de maneira análoga ao procedimento aplicado para o algoritmo SVR.

 

3.1.3 Random Forest Regressor

 

Baseando-se nos excelentes resultados obtidos utilizando o algoritmo de Decision Tree Regressor e visando ainda conseguir ajustes mais refinados, a aplicação deste algoritmo foi sucedida pelo uso do algoritmo Random Forest, que consiste na combinação de diferentes árvores de decisão treinadas em subgrupos da base de dados, de modo a maximizar a variedade dos modelos e combiná-los ao fim para chegar a uma resposta. 

 

Com este algoritmo, aplicando a transformação logarítmica em K para o treinamento e em seguida aplicando a transformação inversa, tal como feito para a segunda aplicação do algoritmo SVR descrito no tópico 3.1.1, chegamos aos seguintes resultados.

 

Com este ajuste computacional, a qualidade dos resultados obtidos foi ainda mais interessante, chegando à um coeficiente de correlação superior à 99,98%, erro médio absoluto de aproximadamente 2,28 e erro médio quadrático inferior à 34,4, aprimorando ainda mais os resultados diante dos algoritmos utilizados até então.

 

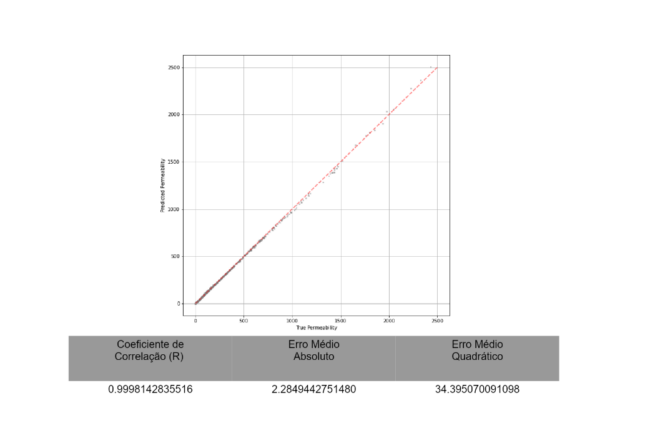
Figura 5 – Predição de Permeabilidade Utilizando Random Forest

 

3.1.4 Multi-layer Perceptron (MLP)

 

Por fim, foi testada a aplicação da rede neural artificial Multilayer Perceptron (MLP), algoritmo famoso que deu base a muitos dos avanços recentes na área de aprendizado de máquina, sobretudo em Deep Learning.

 

Dentre diversas outras aplicações, este modelo computacional já vem sendo aplicado na literatura para processamento e geração de curvas artificiais para logs petrofísicos (BANESHI et al., 2013).

 

Na nossa aplicação, ainda de maneira análoga ao treinamento aplicado aos demais algoritmos, o algoritmo MLP foi aplicado para predizer o valor da permeabilidade em um poço de teste, após ser treinado em uma base de dados composta por outros poços.

 

Esta aplicação obteve os resultados que podem ser ilustrados a seguir:

 

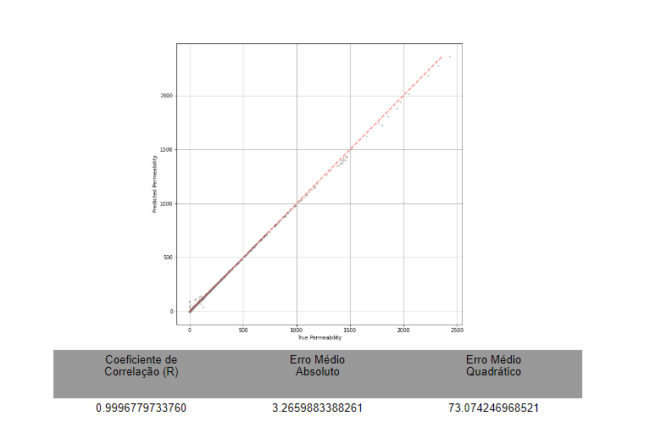
Figura 6 – Predição de Permeabilidade Utilizando MLP

 

3.2 Previsão de Permeabilidade em Carbonatos

 

Esta aplicação foi realizada no contexto de uma bacia sedimentar brasileira off-shore, e o seu intervalo de interesse modelado se refere ao intervalo do pré-sal formado majoritariamente por carbonatos.

 

Aleatoriamente, 80% dos dados foram separados para treino e os 20% restantes para teste.

 

A abordagem proposta inclui as curvas de perfilagem convencionais e a curva de ressonância magnética nuclear.

 

Para cada uma delas, os algoritmos aplicados foram MLP e Random Forest, por terem se mostrado mais promissores após a aplicação anterior.

 

O histograma que mostra a distribuição de frequências dos valores de K existentes na base de dados de treino pode ser visualizado a seguir, na Figura 7:

 

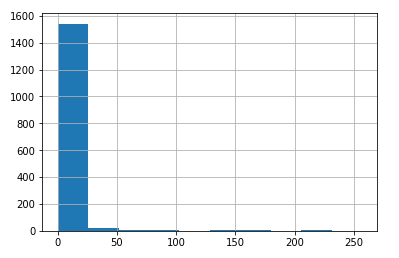
Figura 7 – Histograma para K na base de dados de treino

 

Neste histograma, mostra-se visível uma intensa assimetria nos dados, que dificulta a devida representatividade para o aprendizado do algoritmo.

 

Mesmo aplicando uma transformação logarítmica, ainda não se nota uma mudança significativa na distribuição, tal como pode ser visualizada a seguir:

 

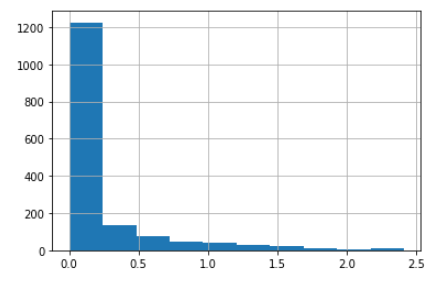
Figura 8 – Histograma para log(K)

 

Embora sabendo que, em primeiro momento, a limitação na base de dados dificultaria o aprendizado dos modelos, o trabalho foi continuado, por compreender que esta seria uma aplicação mais complexa e bons resultados com este modelo poderiam significar boas tendências para aplicação em bases de dados de maior complexidade.

 

A seguir, são definidos e explorados os resultados para a aplicação acima citada, sendo também explorado de maneira gráfica os resultados obtidos e, logo em seguida, as métricas de erro utilizadas para avaliar o desempenho dos modelos, sendo elas o Coeficiente de Correlação (R), Erro Médio Absoluto e Erro Médio Quadrático.

 

3.2.1 Modelagem com Perfis Convencionais e Ressonância Magnética Nuclear (RMN)

 

Considerando, além dos perfis convencionais, os dados do perfil de ressonância magnética nuclear (RMN), aplicamos os algoritmos Random Forest e MLP, visando obter, assim, o valor de permeabilidade para estes poços.

 

Os resultados para esta aplicação, estimando agora para a base de dados de teste o valor de permeabilidade bruto e não mais o logaritmo desta curva, obtemos, na mesma ordem acima apresentada, os resultados ilustrados a seguir:

 

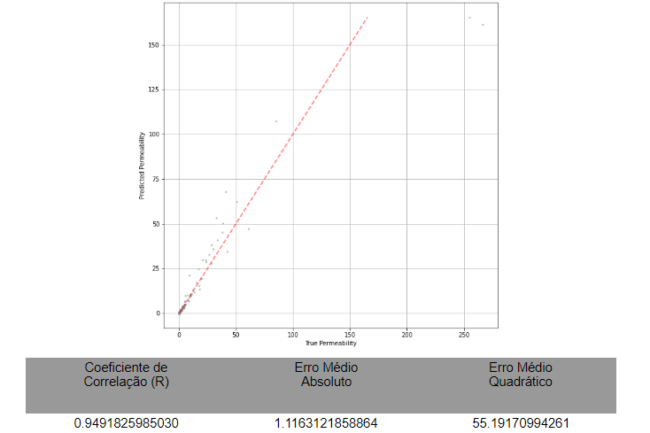
Figura 9 – Predição de Permeabilidade em Carbonatos Utilizando Random Forest

 

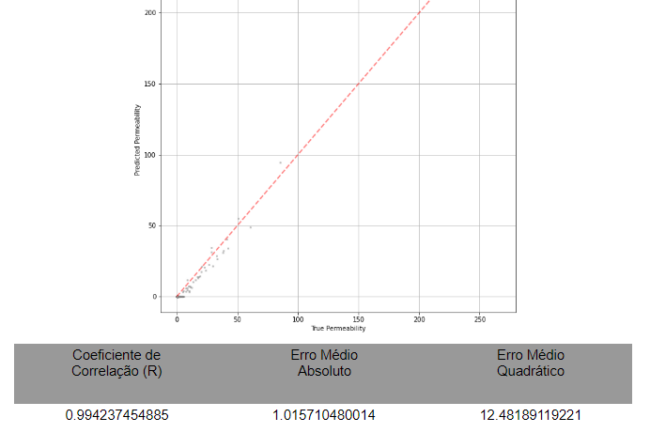
Figura 10 – Predição de Permeabilidade em Carbonatos Utilizando MLP

 

Nesta aplicação em específico, notou-se, sobretudo com o algoritmo MLP, um ajuste consideravelmente bom, apesar das limitações na base de dados.

 

Deste modo, pode-se inferir que, para bases de dados maiores, com maior variedade nos dados, um algoritmo robusto como uma rede neural artificial até mais avançada do que a MLP pode estar apta para tornar esta aplicação ainda mais benéfica e consistente. 

 

Unindo a variedade de modelos desenvolvidos, bem como relacionando estes modelos com outras bases de dados contendo dados de sísmica, de LWD e até mesmo de Mud Logging, pode-se continuar a evolução do nosso sistema para uma plataforma mais robusta e escalável.

 

 

4- Solução Técnica

 

A solução proposta é capaz de prever as curvas de permeabilidade relativa para rochas reservatórios através de técnicas avançadas de aprendizado de máquina. 

 

Qualquer modelo de Machine Learning após treinado em qualquer base de dados é então disponibilizado para os usuários através de uma plataforma web que pode ser acessada através de qualquer computador.

 

Dessa forma, ao dispor dos dados relativos a um poço novo, a permeabilidade pode ser então estimada, analisada e exportada naturalmente através da plataforma.

 

Abaixo podemos observar dois esboços de tela simulando uma situação de funcionamento do sistema.

 

A primeira tela (Figura 11) mostra um exemplo de como o gerenciamento de projetos pode funcionar, podendo ser criados à escolha do usuário e utilizados para agrupar amostras referentes a um mesmo reservatório, ou campo, a critério do usuário.

 

A segunda tela (Figura 12), por sua vez, exemplifica como pode funcionar as estimativas de curvas de permeabilidade.

 

Uma vez inseridos os parâmetros obtidos a partir dos demais ensaios, o sistema irá acessar os modelos de Machine Learning e realizar os cálculos necessários para obtenção dos parâmetros que definem as curvas.

 

Feito isso, a resposta estará pronta para usuário analisar e exportar para uso posterior.

 

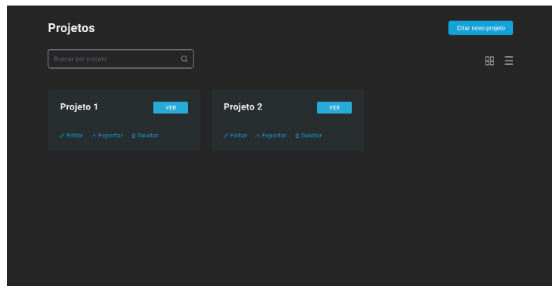
Figura 11 – Interface de Usuário para Gestão de Projetos

 

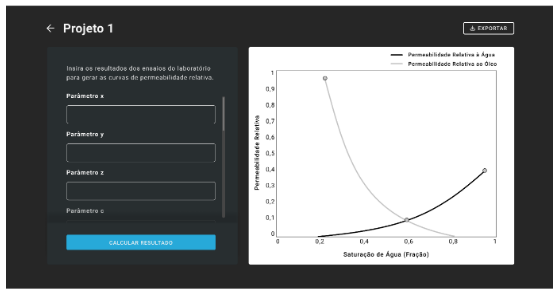
Figura 12 – Interface de Usuário para Análise de Permeabilidade

 

Essa proposta consiste em uma solução customizada para o cliente, capaz de estimar com confiança as curvas de interesse, diminuindo os riscos de exploração, minimizando custos e auxiliando na tomada de decisão, além de possuir a possibilidade de atualização contínua dos modelos preditivos.

 

A longo prazo, o sistema, com os dados do usuário, permite um ajuste fino dos modelos à medida que novas bases de dados sejam utilizadas para treinamento do algoritmo e mantendo sempre o máximo padrão de segurança de dados.

 

Esse fator permite também, caso desejável, que os modelos treinados sejam exportados para que possam ser utilizados em softwares proprietários e em outras aplicações de interesse do cliente, através de técnicas de transfer learning e online learning, aumentando ainda mais sua aplicabilidade no ramo da indústria do petróleo.

 

 

5- Considerações Finais

 

A solução proposta baseia-se, metodologicamente, em uma solução com análise de dados e aprendizado de máquina embarcado em um sistema Web.

 

Diversos algoritmos de aprendizado de máquina, uma vez treinados ou retreinados em uma base de dados conhecida, tornam-se altamente eficientes para identificar padrões e replicar comportamentos.

 

Além disso, estes algoritmos associam o aprendizado dos padrões em uma estrutura de dados complexa composta por camadas, hiperparâmetros e pesos que podem ser serializados e exportados para outras plataformas e aplicações, processo este denominado de transferência de aprendizado.

 

Através da transferência de aprendizado dos modelos treinados e validados e embarcando estes algoritmos em um servidor web, a solução desenvolvida torna-se extremamente eficiente e escalável, aproveitando-se ainda das diversas tecnologias web centradas para maximização da qualidade de interfaces interativas, robustez e segurança da informação.

 

Diante do exposto no presente relatório, é possível perceber a proficiência da equipe executora em resolver problemas petrofísicos utilizando soluções de Machine Learning, bem como proficiência em compreender como utilizar dados relacionados.

 

Com todo esse comprometimento, a Quantageo mostra mais uma vez estar apta a enfrentar e vencer os desafios da Indústria 4.0, entendendo “vencer” como um objetivo centrado em 4 pilares: Valor, Eficiência, Rapidez e Segurança.

 

REFERÊNCIAS BIBLIOGRÁFICAS

 

AL-ANAZI, A. F.; GATES, I. D. Support vector regression to predict porosity and permeability: Effect of sample size. Computers & Geosciences, v. 39, p. 64-76, 2012.

BANESHI, M. et al. Predicting log data by using artificial neural networks to approximate petrophysical parameters of formation. Petroleum science and technology, v. 31, n. 12, p. 1238-1248, 2013.

EL-SEBAKHY, Emad Ahmed et al. Support vector machines framework for predicting the PVT properties of crude oil systems. In: SPE Middle East oil and gas show and conference. Society of Petroleum Engineers, 2007.

LI, Wenrui et al. Seismic data classification using machine learning. In: 2018 IEEE Fourth International Conference on Big Data Computing Service and Applications (BigDataService). IEEE, 2018. p. 56-63.

ROUBICKOVA, Anna; BROWN, Nick; BROWN, Oliver. Using machine learning to reduce ensembles of geological models for oil and gas exploration. In: 2019 IEEE/ACM 5th International Workshop on Data Analysis and Reduction for Big Scientific Data (DRBSD-5). IEEE, 2019. p. 42-49.

 

 

 

 

 

Geoscientists | Geological Data Center | Inteligência Artificial | Machine Learning | Internet das Coisas  

 

 

 

 

 

 

 

Quantageo Tecnologia Ltda.
CNPJ 40.005.610/0001-00
Copyright © 2021